How to solve diophantine equations?

I want to show you a method how to solve linear diophantine equations. The method works for equations in any number of variables. What if the “any number” is $1$ ? Well, if a linear equation of the form $a x=b$ is given with the integers $a, b$ , then if $a$ is zero, then $b$ is zero, too, and every $x$ in the domain is a solution. On the other hand, if $a$ is different from zero, then the only solution is $b/a$ , which may or may not be an integer. Hence, from our point of view the linear equations in one unknown are completely uninteresting.
$solving-diophantine-equations-my-math-4-you$
The next simplest case is of the equations in two unknowns: $a x+b y=c$ . Here we shall suppose that $a, b, c$ are integers and we are looking for integer solutions $x$ and $y$ . So, when talking about a “solution” of our equation we always mean “integer solution”. We also suppose that $a$ and $b$ are different from zero: otherwise we have an equation with less than two unknowns — we’re done with that case.

Considering integer numbers divisibility is the most powerful tool. In our case it is clear that any number which divides both $a$ and $b$ also divides $c$ — no matter what $x$ and $y$ are. In other words, if the numbers $a$ and $b$ have a common divisor which does not divide $c$ , then the equation has no solution. On the other hand, as every common divisor of $a$ and $b$ is a divisor of their greatest common divisor, abbreviated as gcd, we have a necessary condition for the solvability of our equation: the gcd of $a$ and $b$ divides $c$ . For instance, the diophantine equation $4 x+6 y=7$ has no solution. This is clear, as the left side is always an even number, no matter what $x$ and $y$ are.

This is great! Given an equation of the above form it is extremely easy to check if this condition is satisfied — if not, then we are done, there is no solution. But what if the condition is satisfied? “Necessary” does not mean “sufficient”: maybe our condition does not guarantee the existence of a solution, maybe the “necessary” is not “sufficient”. So, from now on we suppose that the gcd of $a$ and $b$ divides $c$ — then we can divide both sides of our equation by this gcd to obtain a similar equation, just the corresponding new $a$ and $b$ have gcd $1$ . And this new equation is equivalent to the original one, which means that they have the same solutions. Consequently, we can simplify our problem by assuming that in the original equation $a$ and $b$ are relatively prime numbers: their gcd is $1$ . Then the original necessary condition is automatically satisfied: $1$ divides $c$ , no matter what $c$ is.

Now our job is to find whole numbers $x, y$ such that $a x+b y=c$ . It is obvious that the expression $a x+b y$ takes both positive and negative values; let $d$ denote its smallest positive value. A fundamental property of the natural number system is the Well Ordering Principle: every non-empty set of natural numbers has a smallest element. So, when considering all positive numbers of the form $a x+b y$ with some integer numbers $x, y$ then there is a smallest one of them which will be denoted by d. In other words, we have $a x+ b y = d$ with some integers $x$ and $y$ , and $d$ is the smallest positive number with this property. We will show that $d$ divides both $a$ and $b$ .

Here we use another basic tool which works in the world of integers: the Division Algorithm. It says that we can find integers $q$ and $r$ such that $a=q d+r$ , where $0 \leq r < d$ . This is the well-known algorithm which produces the quotient $q$ and the remainder $r$ . In this case we have

$r=a - q d=a - q(a x+ b y)= a(1-q x)+b (- q y).$

We use this silly form to emphasize that $r$ is also a possible value of the expression $a x+b y$ — we just replace $x$ by $1-q x$ and $y$ by $- q y$ . As $r$ is non-negative and smaller than $q$ , hence, by the choice of $d$ it must be zero: $r=0$ . This means that $a$ is divisible by $d$ . By similar reasoning we have that $d$ divides $b$ , too. Thus $d$ is a common divisor of $a$ and $b$ . On the other hand, if $c$ is any common divisor of $a$ and $b$ then we have $a= c u$ and $b= c v$ with some integers $u, v$ , consequently

$d=a x+b y=c u x+c v y.$

Thus shows that $c$ divides $d$ , hence the positive number $d$ has the following crucial properties: it is a common divisor of $a$ and $b$ , and it is divisible by any common divisor of $a$ and $b$ . In other words, $d$ is exactly the greatest common divisor of $a$ and $b$ — in our case it is $1$ .

Oops! We have proved that if $a$ and $b$ are relatively prime numbers than the equation $a x+b y=1$ has a solution $x, y$ in the integers. Going back to the original problem, we have proved that if the gcd of $a$ and $b$ divides $c$ , then $a x+b y=c$ has a solution $x, y$ in the integers. Summarizing, we completely proved the following necessary and sufficient condition about the solvability of diophantine equations:

Theorem
Given the whole numbers $a, b, c$ the equation $a x+ b y=c$ is solvable in the set of whole numbers if and only if the greatest common divisor of $a$ and $b$ divides $c$ .

For instance, the equation $7 x - 4 y = 6$ has integer solutions, but the equation $6 x+ 9 y = 8$ does not have. It’s good to know before we start to find a solution. Also, as a consequence we have that $a x + b y = d$ is always solvable if $d$ is the greatest common divisor of $a$ and $b$ . Another corollary is that if $a$ and $b$ are relatively prime numbers, then every integer can be written in the form $a x+ b y$ with some whole numbers $x, y$ .

There is only one open question left: how to find the solutions if they exist? We present a solution method on the following example: $5 x+ 22 y = 18$ . Here the gcd of $5$ and $22$ is $1$ , hence the equation is solvable. We write the equation in the following form:

$5x = 18 - 22 y,$

in other words, we express that term of $a x$ and $b y$ where the absolute value $|a|$ or $|b|$ is smaller. If they are equal, then we can choose any of them. Now we write our equation in the form

$x =\frac{18-22y}{5} =\frac{15-20y}{5}+\frac{3-2y}{5}=3-4y+\frac{3-2y}{5}.$

In other words, we separate those terms which are clearly divisible by $5$ , divide them by $5$ , and then we have the remainder $\frac{3-2y}{5}$ . As $x$ is a whole number, hence $3-2 y$ is divisible by $5$ , that is $3-2 y = 5 z$ with some integer $z$ . We can write this in the form $2 y + 5 z = 3$ . Now we repeat the above process: we express $2 y$ :

$2 y =3 - 5 z, y = 1- 2 z +\frac{1-z}{2}.$

Again, $y$ is an integer, hence $1-z$ is divisible by $2$ , that is $1 - z = 2 u$ with some integer $u$ . We infer $z =1-2 u$ , and by the previous equation it follows

$y=1- 2(1-2 u)+u=5 u-1.$

Going back to $x$ we have

$x= 3 - 4 y+z= 3 -4(5 u-1)+1 - 2 u=8 - 22 u.$

Finally, we have the solution $x, y$ in the form

$\begin{eqnarray*} x &=& 8 - 22 u\\ y &=& 5 u - 1, \end{eqnarray*}$

and here $u$ can be an arbitrary whole number. It is easy to check that $x, y$ form a solution no matter what is $u$ :

$5 x + 22 y=5(8 - 22 u)+22 (5 u - 1)=40 -110 u+ 110 u - 22=18.$

And our process shows that indeed, every solution must have this form with some $u$ . In the above solution $u$ is an integer parameter, and as $u$ runs through the set of all integers the points $(8 - 22 u, 5 u - 1)$ run through all points with integer coordinates on the straight line $5 x + 22 y = 18$ .

From this all we have to remember the following crucial facts:

The Well Ordering Principle, which says that any non-empty set of natural numbers has a smallest element. Think about this! If you want to prove this statement somehow, then you will see that the reason is that in the world of natural numbers there is no infinite strictly decreasing sequence. No matter where you start, if you pick smaller and smaller natural numbers, then your process will terminate after a finite number of steps. The integers do not have this property: we can take the negative integers 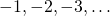$-1, -2, -3,\dots$ etc., and this process never terminates, there is always a smaller one. You may think that this is because there is a smallest natural number: 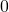$0$ , but there is no smallest integer number. No, no, this is not the reason, as it is shown by the example of rational numbers. Non-negative rational numbers have a smallest number, the zero, but still we can construct infinite decreasing sequence of non-negative rational numbers: for instance, the reciprocals of positive integers have this property. The Well Ordering Principle is a very own property of the natural number system.
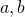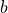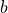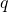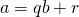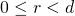The Division Algorithm, which says that given two whole numbers $a, b$ with $b$ is non-zero then $a$ can be divided by $b$ with remainder in a unique way: we can always find two unique whole numbers $q$ and $r$ such that $a = q b + r$ , and $0 \leq r < d$ . Here we call 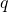$q$ the quotient and $r$ the remainder.

Vélemény, hozzászólás? Válasz megszakítása

Hozzászólás küldéséhez be kell jelentkezni.