The tricky Prince

Carl Friedrich Gauss, the German mathematician, one of the „Greatest of the Greats”, who is often referred to as the Princeps mathematicorum, the foremost of mathematicians had an exceptional influence in many fields of mathematics and science, and is ranked among history’s most influential mathematicians. There are different anecdotes about his early genius.
$gauss-sequences-my-math-4you$
According to one of them, in primary school after the young Gauss misbehaved, his math teacher requested him to add the list of integers from 1 to 100. The teacher thought it would take a while to complete the task but the young genius produced the correct answer within seconds. The teacher was bluffed and — according to the anecdote — he asked the young guy how he did it. Gauss’s method was to add 1 to 100, then 2 to 99, the 3 to 98, continuing up to 50 to 51, and as all these sums of pairs have the common value 101, and there are exactly 50 pairs of this type, the total sum is 50 times 101, which is 5050.

What is the „moral” of this story? In fact, the young Princeps gifted us the general method of summing up arithmetic progressions. What is an arithmetic progression? Well, the simplest arithmetic progression is presented by the sequence of natural numbers: 1, 2, 3,… Here the progression is realized by adding the same number, the number 1 again and again to each term in order to get the next one. The emphasis is on „the same number”: in fact, we call a sequence of numbers an arithmetic progression if the similar property holds: starting with any number each term of the sequence is obtained from the previous one by adding always the same number, called the difference of the progression.

Clearly, any arithmetic progression is completely determined by its starting term and by its difference. In general, an arithmetic progression can be both finite or infinite: for instance, the sequence of natural numbers, mentioned above, is an infinite arithmetic progression, but we can stop at any number obtaining a finite arithmetic progression.

Obviously, a nontrivial arithmetic progression must contain at least three terms. Arithmetic progressions show up very frequently in mathematics, in sciences, as well as in everyday life. We underline that the terms of the arithmetic progression can be arbitrary real numbers, and also the difference can be any number: positive, negative or even zero. In the last case the „progression” can be characterized as „nothing happens”: all terms of the sequence are equal. Positive differences provide increasing progressions, while the negative ones correspond to the decreasing „progressions”, which are rather „regressions”.

Arithmetic progressions have nice properties — some of them even characterize this concept. One characteristic property is that if we choose any term of such a progression, and two terms which are located in the sequence symmetrically with respect to this term then the average of these two latter terms is the one we started with. In mathematical terms, if $a_n$ is any term of the sequence, then for each natural number $k$ which is less than $n$ the average of $a_{n-k}$ and $a_{n+k}$ is exactly $a_n$ . So, if we go $k$ steps forward and $k$ steps backward from the $n$ -th term then the average of the two terms obtained in this way is equal to the $n$ -th term. No matter how many steps we go forward and backward.

This „three-term-property” can easily be generalized for any odd number of terms: if they are located in the sequence symmetrically with respect to the one in the middle, then the average of all terms is equal to the one in the middle. The average is nothing but the arithmetic mean, which we discussed in a former post. As a simple consequence we have that if we have a finite arithmetic progression then the average of all terms in this progression is equal to the average of the starting term and the last term. Or the average of the second term and the last but one term. Or… and so on.

If you have a look at the last problem, Problem 20 of the 2018 Easter Math Challenge then you can utilize this observation to solve that problem very quickly. Indeed, the question is which set of numbers has the largest average: the multiples of 2, or 3, or 4, or 5, or 6 between 1 and 101? Clearly, these multiples in each case form an arithmetic progression, hence in the light of our previous observation the average of these sets of numbers can be replaced by the average of the largest and the smallest number in the set, or simply by the sum of these two numbers. In the case of multiples of 2 between 1 and 101 it is 2+100=102, then in the case of multiples of 3 between 1 and 101 it is 3+99=102, then similarly, we have 4+100=104, and 5+100=105, and finally 6+96=102. The largest sum occurs in the case of 5 — this is the correct answer!

You may ask now how this all relates to Gauss — but I hope you’ll get the answer immediately. Yes, the teacher of the naughty genius wanted him to sum up the arithmetic progression of the natural numbers from 1 to 100. The sum of all terms is clearly equal to their average multiplied by the number of terms — and Gauss figured out immediately that the average is equal to the average of the first and the last term: the half of (1+100)/2, and multiplying by the number of terms, which is 100 we get the blitz result: 50 times 101=5050.

There are some other simple questions about arithmetic progressions: one of them is how to compute the $n$ -th term if the starting term and the difference is given? You may say that this is obvious: consecutively we add the difference to the starting term and we stop after… — how many additions? The second term is obtained by one addition, the third by two additions, etc., hence the $n$ -th term is obtained by adding the difference $n-1$ times to the starting term. In other words: $a_n=a_1+(n-1)d$ , where $d$ denotes the difference.

Another basic question is whether two different terms determine the progression uniquely? The idea is that if we plot the terms of an arithmetic progression in a coordinate system, then all the terms will lie on a straight line: this is the consequence of the linear character of the previous formula. Moreover, geometrically it is clear that a straight line is uniquely determined by any two different points on the line. Well, a straight line is infinite, and it is uniquely determined by a point on the line and by the slope. However, in the case of arithmetic progressions, even in the infinite case, we need a starting term: two different terms determine the „slope” only, which is the difference of the progression.

On the other hand, if we know the „rank”, i.e. the serial number of the terms, that is not just $a_n$ and $a_m$ but also $n$ and $m$ , then we are done: indeed, from the above formula we have

$d=\frac{a_n-a_m}{n-m},$

and finally $a_1=a_n-(n-1)d$ .
\vskip.2cm

Still another related problem is how to sum up all terms of an arithmetic progression, which makes sense only if the the sequence is finite. We should perform the following operation:

$S_n=a_1+a_2+a_3+\dots+a_{n-1}+a_n,$

where $S_n$ denotes the sum of the first $n$ terms of the arithmetic progression with difference $d$ . Clearly, we can use the formulas:

$\begin{eqnarray*} a_1&=&a_1+0\cdot d\\ a_2&=&a_1+1\cdot d\\ a_3&=&a_1+2\cdot d\\ ...&=&...\\ ...&=&...\\ a_{n-1}&=&a_1+(n-2)\cdot d\\ a_n&=&a_1+(n-1)\cdot d, \end{eqnarray*}$

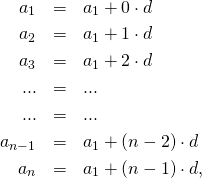
and sum up these equations to get

$S_n=n\cdot a_1+(0+1+2+\cdots+(n-1)+n)\cdot d,$

which is not very nice due to the dots on the right side. Here we can apply Gauss’s method: how did it work exactly? He added the first term to the last, the second to the last but one, etc. He had good luck, as the number of the terms was an even number, hence each term had a pair. Finally, he summed up the sums of all pairs. We can modify his method just a little bit so that it works also in any case, no matter of the number of the terms is even or odd. In fact, we write $S_n$ in two different ways:

$\begin{eqnarray*} S_n&=&a_1+\,a_2\,\,\,\,\,+\,\,a_3\,\,\,+\dots\,\,\,+a_{n-1}+a_n\\ S_n&=&a_n+a_{n-1}+a_{n-2}+\dots\,\,\,+\,a_2\,\,+a_1, \end{eqnarray*}$

using increasing, and decreasing order of the subscripts. Now we can add the two equations to get

$2 S_n=(a_1+a_n)+(a_2+a_{n-1})+(a_3+a_{n-2})+\dots+(a_{n-1}+a_2)+(a_n+a_1),$

where in the brackets the sum of the subscripts is always $n+1$ . And now we apply what we have seen above: the sums in the brackets are all the same! Hence we can write

$2 S_n=n\cdot (a_1+a_n),$

and finally

$S_n=n\frac{a_1+a_n}{2},$

which expresses the obvious fact that the sum of the first $n$ terms equals $n$ times the average of the pairs which are located symmetrically to the „middle” of the progression, no matter if this „middle” is a term of the sequence, or not. This formula expresses the sum of the first $n$ terms using the first term, the last term and the number of terms. We can apply this last formula for the Gauss–job to get

$S_{100}=100\,\frac{1+100}{2}=50\cdot 101=5050.$

If we want to use the first term and the difference only, then we can replace $a_n$ by $a_1+(n-1)d$ to get the other form of this sum:

$S_n=\frac{n}{2}\bigl(a_1+a_1+(n-1)d\bigr)=n\cdot a_1+ \frac{n(n-1)}{2} d.$

Now you can check yourself: are you ready to solve problems about arithmetic progressions? Following the tricky Prince? Ready, steady — go to the problems!